Abstract
This entry considers William Playfair’s invention of statistical graphics, which turns dates into data and thus helps users to recognize new kinds of events. Because their arresting visual features are designed to save time for men of “rank or active business,” the graphs respond to an increasing sense of acceleration and information overload that we associate with emergent modernity. Despite being of their moment in this way, the graphs failed to catch on, and the explanation for this underscores this entry’s framing questions about changing understandings of date and event in the period covered by the BRANCH project.
Traditionally when we think about an historical event we think about something that happened, something unique and distinctive, something to which we can assign a date, a set of causes, a series of individual actions and intentions, possibly with unintended consequences, that collectively can then be grouped under a single referent like “The French Revolution” or the “English Civil War.” Events of this sort have a narrative, a set of beginnings, middles, and ends that can be disputed but that ultimately connect their elements into a coherent arc, one that separates this event (the French Revolution, say) from that event (the Seven Years War), while also indicating the place of a particular event in a longer series of events to which it is related (![]() France in the eighteenth century). Herbert F. Tucker’s engaging meditation on eventfulness, “In the Event of a Second Reform,” highlights these issues with great perspicuity. He suggests that this common understanding of event might be understood as Aristotelian, since the significance of an event lies in its capacity to transmit its force to another event that follows from it. An event, in Tucker’s description, thus implies a before and an after that are essential to its intelligibility but also exterior to the event itself. Events in this description are emplotted, discursive, and therefore “Poetic.”[1]
France in the eighteenth century). Herbert F. Tucker’s engaging meditation on eventfulness, “In the Event of a Second Reform,” highlights these issues with great perspicuity. He suggests that this common understanding of event might be understood as Aristotelian, since the significance of an event lies in its capacity to transmit its force to another event that follows from it. An event, in Tucker’s description, thus implies a before and an after that are essential to its intelligibility but also exterior to the event itself. Events in this description are emplotted, discursive, and therefore “Poetic.”[1]
Tucker’s account calls particular attention to the constructed quality of historical events, to the manner in which their seeming coherence is assigned and framed by later interpreters. Although eighteenth- and early nineteenth-century thinkers would not have shared this emphasis on constructivism, the narrative and discursive understanding of history described by Tucker was certainly the dominant understanding of history and historical events in the eighteenth century. At the end of the eighteenth century, however, another model of historical interpretation began to emerge, one that relied not on a narrative of seemingly unique events but instead on the standardization and repetition of events and episodes that, while seemingly insignificant in themselves, could be perceived as significant in their aggregate. This is a model related to the growth of statistics and what we now call the social sciences, one that relies on data and one that might be described as fundamentally informational. It is, further, a model in which the status of an event comes to have a very different significance.
This entry attempts to show some of the implications of this emergent model of historical interpretation as it bears on our understanding of an event by looking at the development of statistical graphics: techniques for illustrating numerical quantities as lines or geometric shapes like the bar chart, the circle chart, or the pie chart, and similar techniques, like the time-series line graph, meant to show changes in such quantities over time. While today’s users of spreadsheets may take for granted the ease with which tables of numbers can be turned into lines or shapes and interpreters of economic data would find it virtually impossible to make arguments without the aid of such techniques for data visualization, few are aware that all three techniques were popularized (if not outright invented) by William Playfair between 1786 and 1801.[2]>
Two of the most striking features of Playfair’s diagrams are, first, that Playfair’s work was so definitive that, as one leading scholar of statistical graphics notes, “time-series line graphs are seen in essentially the same form as today” (Spence, 2006, 2427); and, second, that despite their apparent prescience, they failed to catch on and had virtually no impact or imitators in England until William Jevons began to engage Playfair’s work in the later nineteenth century.[3] In the third edition of the Commercial and Political Atlas (1801), Playfair claimed that he was “the first who applied the principles of geometry to matters of Finance” (viii). This may be true, but Playfair’s use of lines and circles does not rely on advanced geometric principles, nor was he the first to plot figures on a Cartesian coordinate system.[4] What is important about Playfair, however, is that unlike most of his predecessors, who used the abscissa (x-axis) and ordinate (y-axis) coordinates to plot abstract mathematical functions, Playfair was a pioneer in his use of graphs to represent empirical historical data, and he thus becomes a particularly interesting figure through which to think about late eighteenth-century changes in the understanding of history and the meaning of an event more generally. Because Playfair’s charts rely on aggregate empirical data and the repetition of a particular kind of measurable commercial event (exports and imports) over a series of annual dates (years), they raise questions about whether the potential significance of an event lies in its uniqueness or its repeatability. A focus on such historiographical issues, this entry will suggest, might also help to explain why it took so long for others to imitate or develop Playfair’s work.
William Playfair: Life
Playfair is an intriguing character who led a colorful life. He was the younger brother of John Playfair, the champion of James Hutton’s Theory of the Earth (1788) who succeeded Dugald Stewart as professor of mathematics at ![]() Edinburgh University. William’s career, however, was much less conventional than that of his older brother. While John Playfair stayed in
Edinburgh University. William’s career, however, was much less conventional than that of his older brother. While John Playfair stayed in ![]() Scotland, William Playfair apprenticed first for three years with Andrew Meikle (the inventor of the drum threshing machine in 1789) and then with Matthew Boulton and James Watt (the improver of the steam engine) in
Scotland, William Playfair apprenticed first for three years with Andrew Meikle (the inventor of the drum threshing machine in 1789) and then with Matthew Boulton and James Watt (the improver of the steam engine) in ![]() Birmingham. Eventually, he abandoned engineering for enterprise and set off for France, where the 1789 translation into French of his Commercial and Political Atlas (1786) had attracted the attention of Louis XVI. In France, he stayed through the Revolution (and was rumored to have stormed the
Birmingham. Eventually, he abandoned engineering for enterprise and set off for France, where the 1789 translation into French of his Commercial and Political Atlas (1786) had attracted the attention of Louis XVI. In France, he stayed through the Revolution (and was rumored to have stormed the ![]() Bastille), became involved in the notorious Scioto land swindle, and left to escape prosecution just before the Terror. Back in London, his various enterprises included a bank, a newspaper, gun-carriage making, and a series of dubious efforts to supplement his income by blackmail, extortion, and one outright swindle that led to his conviction at the court of the King’s Bench in 1805—the same year that he published his most ambitious work, the Inquiry into the Permanent Causes of the Decline and Fall of Powerful and Wealthy Nations, and also the first critical edition of Smith’s Wealth of Nations, which included corrections and extensions of Smith’s ideas. Today, Playfair is best known for his contributions to statistical graphics, especially the time-series line graph, the bar chart, and the pie chart.[5]
Bastille), became involved in the notorious Scioto land swindle, and left to escape prosecution just before the Terror. Back in London, his various enterprises included a bank, a newspaper, gun-carriage making, and a series of dubious efforts to supplement his income by blackmail, extortion, and one outright swindle that led to his conviction at the court of the King’s Bench in 1805—the same year that he published his most ambitious work, the Inquiry into the Permanent Causes of the Decline and Fall of Powerful and Wealthy Nations, and also the first critical edition of Smith’s Wealth of Nations, which included corrections and extensions of Smith’s ideas. Today, Playfair is best known for his contributions to statistical graphics, especially the time-series line graph, the bar chart, and the pie chart.[5]
William Playfair: Works
The full title of Playfair’s first major publication from 1786 makes its objectives plain: The Commercial and Political Atlas, Representing by Means of Stained Copper-Plate Charts, the Progress of the Commerce, Revenues, Expenditure, and Debts of England, During the Whole of the Eighteenth Century. The Atlas was reprinted in 1787, with a third edition, which updates the charts through the end of the eighteenth century and offers an expanded introduction, appearing in 1801. The ambitious scope of the Atlas, its promise to address comprehensively England’s state finances for, as its title indicates, “the whole of the eighteenth century,” is made possible by a sequence of time-series line graphs, each of which is followed by textual observation and commentary. The first chart, for example, shows the sum totals of England’s imports and exports across the eighteenth century. (See Fig. 1.)
The horizontal axis represents one hundred years and is subdivided neatly by dark vertical lines at ten-year increments. From 1760 forward, a series of lighter vertical lines represent individual years. The vertical axis shows quantities of money in millions of pounds, with darker horizontal lines emphasizing increments of ten million pounds. The line mapping the monetary value of exports has been colored red, while that of imports is colored yellow. The shaded area between them, when the balance is in favor of England, is shaded green, and for the brief moment ca. 1781 when the balance is against, the area has been shaded red. In the charts that follow, the same technique is applied to illustrate England’s trade balance with particular countries and regions: ![]() Ireland, the East Indies, the West Indies, North America, France,
Ireland, the East Indies, the West Indies, North America, France, ![]() Spain,
Spain, ![]() Germany, etc. A subsequent section of the work is titled “Public Accounts” in 1786 and 1787, which changes to the “Financial Part of the Political Atlas” in 1801. It contains a chart comparing the revenues of England and France from 1550 to 1800; a chart of the national debt from 1688 to the present; a chart showing the effect a sinking fund would have on the debt projected forward through the nineteenth century; a chart of fees paid for services from 1722 to 1800; charts showing expenditure on the navy, the army, and the ordnance from 1720 to 1800; before concluding with a chart of the price of flour over the past ten years.[6]
Germany, etc. A subsequent section of the work is titled “Public Accounts” in 1786 and 1787, which changes to the “Financial Part of the Political Atlas” in 1801. It contains a chart comparing the revenues of England and France from 1550 to 1800; a chart of the national debt from 1688 to the present; a chart showing the effect a sinking fund would have on the debt projected forward through the nineteenth century; a chart of fees paid for services from 1722 to 1800; charts showing expenditure on the navy, the army, and the ordnance from 1720 to 1800; before concluding with a chart of the price of flour over the past ten years.[6]
In each edition of the Atlas, Playfair observes the correlation between cartography and graphic statistics, a connection underscored by his use of the term “atlas” to describe his visual techniques. “The amount,” he notes, “of mercantile transactions in money, and of profit or loss, are capable of being as easily represented in drawing, as any part of space, or as the face of a country; though, till now, it has not been attempted. Upon that principle these Charts were made” (Playfair, 1786, 3).[7] This claim is then cited directly in the expanded introduction to the third edition (1801). The third edition further explains the technique Playfair calls “lineal arithmetic” through the hypothetical example of a merchant paid solely in guineas. This merchant could make a single pile of all the guineas collected on a given day, and, if left in place over time, each pile would enable a quick comparison of the revenues on a day-by-day basis. “Lineal arithmetic,” Playfair concludes, “is nothing more than those piles of guineas represented on paper, and on a small scale, in which an inch (suppose) represents the thickness of five millions of guineas, as in geography it does the breadth of a river, or any other extent of country” (xi).
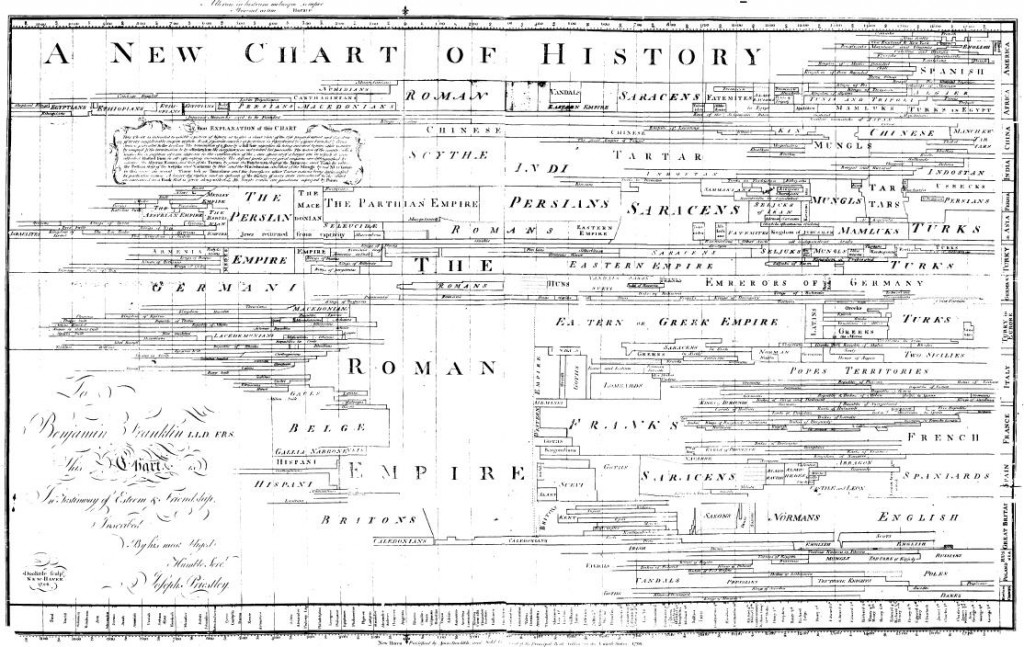
Playfair emphasizes that any number can be represented by a scaled line. He would later credit this insight to his brother, John, who “made me keep a register of a thermometer, expressing the variations by lines on a divided scale. He taught me to know, that, whatever can be expressed in numbers, may be represented by lines” (Playfair, 1805, xvi). The idea may also be linked to Joseph Priestley, who utilizes it first in his Chart of Biography (1765) and then in his more ambitious (and more visually arresting) New Chart of History (first ed. 1769, second in 1770). Each of these works anticipates Playfair’s assumption that every numerical quality (the years of a life or the duration of a historical event) could be readily translated into a line—which is also the organizing principle of any timeline. In his companion description to the New Chart of History, Priestley, like Playfair after him, used geographic analogies and argued that all time could be represented as a line. “Time here,” Priestley insists, “flows uniformly, from the beginning to the end of the tablet. It is also represented as flowing laterally, like a river. . .” (8). With a horizontal axis of years and a vertical axis of territories, Priestley aspired to the visual equivalent of universal history. (See Fig. 2.)
He hoped to show both the temporal duration and the spatial expanse of empires in a glance, and hence to impress the imagination “indelibly” and efficiently with “a just image of the rise, progress, extent, duration and cotemporary state of all the considerable empires that have ever existed in the world” (11). Looking horizontally would show all the changes across time in the government of a particular territory, while a vertical glance allowed for the comparison of various territories.[8]
The problem with Priestley’s chart, however, is that while it could show which kingdoms occupied which territories, it had no way accurately to show the size of a kingdom’s territory in comparative scale with other kingdoms and hence no graphic means of showing what Priestley above calls “extent.” Priestley himself recognized the issue. He noted further that to include large spaces like Tartary, ![]() Siberia, and America, places that he describes as “barren of events,” would distort the chart’s scale and make it “immoderately large” (16). This is a problem that would subsequently be solved by Playfair, who enhanced Priestley’s historical chart and extended its linear and geometric principles to the financial measurement of relative prosperity and decline. He also devised a means of using a uniform geometric figure (the circle) to produce a ready comparison of the sizes of disparate territories, as discussed below. That Playfair drew from Priestley’s work should not be surprising. When Playfair apprenticed with Boulton and Watt, he would have been exposed to the members of their circle, which included Priestley.[9]
Siberia, and America, places that he describes as “barren of events,” would distort the chart’s scale and make it “immoderately large” (16). This is a problem that would subsequently be solved by Playfair, who enhanced Priestley’s historical chart and extended its linear and geometric principles to the financial measurement of relative prosperity and decline. He also devised a means of using a uniform geometric figure (the circle) to produce a ready comparison of the sizes of disparate territories, as discussed below. That Playfair drew from Priestley’s work should not be surprising. When Playfair apprenticed with Boulton and Watt, he would have been exposed to the members of their circle, which included Priestley.[9]
Repeatedly, Playfair insists on the psychological efficacy of the graphic representation of quantitative information. To see numerical data as geometric shapes, he asserts, reveals its significance more quickly, makes it easier to remember, and saves time for those “of high rank, or active business” (Atlas, 1801, xiv). To aid this endeavor and to initiate the unfamiliar, he offers a brief explanation of how to use his charts so that “those who do not, at first sight, understand the manner of inspecting the charts” can read “the few lines of directions facing the first Chart, after which they will find all the difficulty entirely vanish, and as much information may be obtained in five minutes as would require whole days to imprint on the memory, in a lasting manner, by a table of figures” (Atlas, 1801, xii; emphasis original).[10]>
The emphasis is on the time-saving qualities of visualization. Playfair promises that he can reduce days of work into the space of “five minutes.” Playfair’s charts can thus be understood as a direct response to the profusion of knowledge and information that we associate with the Enlightenment specifically and with the eighteenth century more generally. This seeming explosion of information—the sheer proliferation of raw data—is, of course, what enables Playfair’s time-series graphs. Furthermore, it was the lack of data that produced Playfair’s first bar chart, of Scotland’s imports and exports from 1780-81, which did not include a time element because there was not enough data to support a time-series graph. Playfair observed that “This chart. . . does not comprehend any portion of time, and is much inferior in utility to those that do” (1786, 101), and he removed it from subsequent editions of the Atlas. But, for Playfair, the proliferation of information does more than provide raw data for visualization, it practically mandates such techniques and is necessary for those busy men with increasing demands on their time: “As knowledge increases amongst mankind, and transactions multiply, it becomes more and more desirable to abbreviate and facilitate the modes of conveying information from one person to another, and from one individual to the many” (Atlas, 1801, vii). Playfair even imagines that the charts overcome the problem of language because vision, in his reckoning, is commensurate with a universal language; translated into geometrical shapes and charts, his information can be transmitted such that even “a native of another country [might] understand the nature of the business delineated” (Atlas, 1801, v).
In his 1805 work An Inquiry into the Permanent Causes of the Decline and Fall of Powerful and Wealthy Nations, Playfair later reproduced up-to-date versions of three of the charts that had previously appeared elsewhere in his work: the initial chart of British imports and exports from 1700 to 1805 (plate 1 of the Atlas); the comparative increases in annual revenues between Britain and France from 1700 to the present (plate 19 of the 1801 Atlas); and his original circle and pie chart showing the extent of population and revenues in Europe’s principle nations (plate 1 of The Statistical Breviary [1801]). As its title indicates, the Inquiry combines aspects of Smith’s Wealth of Nations (1776) and Gibbon’s Decline and Fall (1776-1788). Playfair surveys historical empires and argues that decline can be measured and thus prevented and forestalled; in particular, he insists that commerce, not conquest, sustains national power and that nations, particularly England, can maintain commercial prosperity if they direct their attention to preservation rather than extension. Particular attention must be paid to managing the national debt and maintaining a trade balance in favor of export.[11] With its prolonged historical survey organized around four central graphs, the Inquiry works verbally and visually. It combines historical scope with measurable, quantifiable data in order to suggest that a proactive government-driven approach to the problem of decline can prolong national wealth and power. Playfair’s focus on national debt and balance of trade may not be unique, but the work is, so far as I can tell, the first attempt at a general and comparative theory of the rise and fall of nations. It has also been described by one economic historian as the first sustained theory of capitalist development (see Grossman).
What further distinguishes the Inquiry is the effort to represent this argument with a series of sophisticated charts. To the three charts reprinted from earlier editions of the Atlas, Playfair added an initial chart spanning three millennia and showing the comparative progress and decline of all known empires, from ancient empires in ![]() Egypt and Assyria through modern empires in Europe and emergent empires in the Americas. (See Fig. 3.)
Egypt and Assyria through modern empires in Europe and emergent empires in the Americas. (See Fig. 3.)
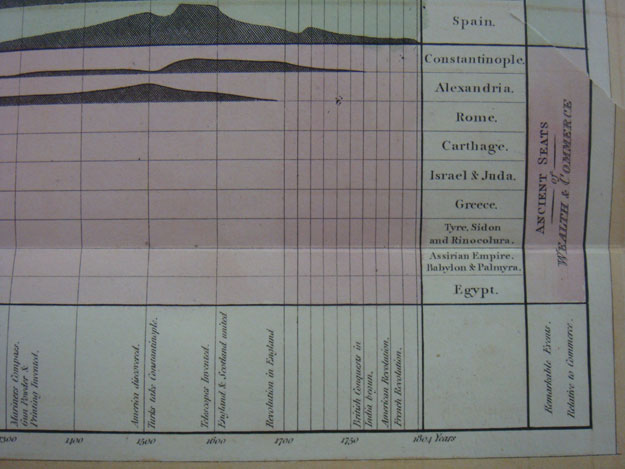
Figure 3: William Playfair, _Inquiry into the Permanent Causes of the Decline and Fall of Wealthy and Powerful Nations_ (1805), figure 1
Here, time extends along its horizontal axis with an even chronology punctuated by “Remarkable Events Relative to Commerce.” The vertical axis shows ancient seats, European seats, and America, all distinguished by colour. Combining the two allows Playfair to illustrate the arc of progress and decline and to offer a visual representation of the universal life cycle of commercial empires (though he markedly excludes the east). Like Priestley’s New Chart, Playfair’s illustrations turn abstract time into something that can be imagined and visualized concretely as a continuous linear progression. The key here is uniformity of scale, a development located in the mid-eighteenth century by Anthony Grafton and Daniel Rosenberg in their recent history of the timeline. “Once that uniformity had been achieved,” they note, “projecting other kinds of quantitative data into the chronographic space was not difficult” (136). It may not have been difficult, but it certainly was not common. Playfair also adds an additional dimension to Priestley’s linearity. Playfair’s circle chart showing the extent of population and revenues in Europe’s principle nations (plate 2 of the Inquiry and plate 1 of the Statistical Breviary), for example, translates irregularly shaped landmasses into uniformly scaled circles whose representations of areas are then further divided into wedges or pies.[12] (See Fig. 4.)
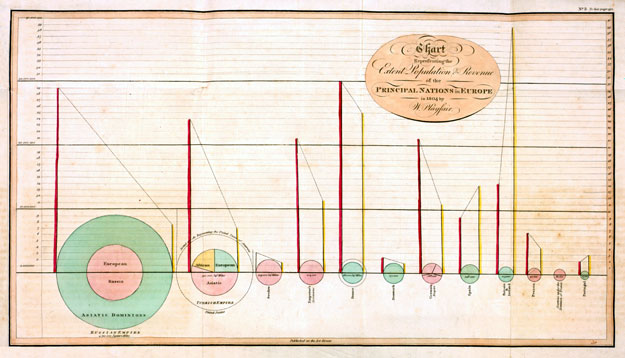
Figure 4: William Playfair, _Inquiry into the Permanent Causes of the Decline and Fall of Wealthy and Powerful Nations_ (1805), figure 2
Each of these circles has two tangent lines, a yellow one for population and a red one for revenue. At a glance, then, one trained to interpret this visual information can make a comparison of the population and revenue of each nation relative to its geographical extent.[13] It is, in the end, a visually innovative way to make the argument that, so long as wealth is defined quantitatively as revenue, it cannot be equated with the extent of a nation’s territory—an argument, in other words, against those who argued that territory and population constituted a nation’s wealth.
Meta-Critical Reflections
Visually arresting, clearly engraved, and colored to make their presentation of information even more clear, Playfair’s charts are striking documents. They are significant for a number of reasons, not the least of which is their conceptual similarity to the BRANCH project. Both BRANCH and Playfair take the year as their organizational principle and suggest that the details of a compounded series of years can produce knowledge about a larger-order temporal formation, a century. To be fair, the knowledge-producing ambitions of BRANCH are more widespread than the financial issues that most concern Playfair, but the juxtaposition between the two raises a further series of questions about scale—questions about the relationship between the year and the century, the annual and the centurial, about the way that the relationship between them is imagined to produce knowledge, and about the scale on which knowledge is produced.
The charts themselves are also of interest for the way that they treat problems of temporality. If we think of the later eighteenth century as a moment of perceived acceleration, a perception fed by the proliferation of data to which Playfair explicitly responds, and a time during which historical actors experienced increasingly complicated relations to temporal processes, a recognition of what Reinhart Koselleck describes as “the peculiar form of acceleration which characterizes modernity” (5), then one of the benefits of Playfair’s graphs is their ability to stop time. They show in a single image an abstract process as it is perceived to develop over a century, one that they then fix and make concrete. But in the way that such charts are scaled, they also participate in and advance the sense of acceleration because they enable viewers to see large swathes of time in a glance. Recall those men of high rank and active business whom Playfair imagines as his audience suddenly enabled to take in as much information in “five minutes” as would require “whole days” if seen as a table. Time itself takes less time to see.
Further, Playfair’s charts emerge at a particular historical moment—the later eighteenth century—that, with the increasing proliferation of print media generally and periodical writing in particular, was becoming an age of serialized, often annualized regularity. In the face of an increasingly uneven temporal experience, the publication of periodicals was evenly spaced and they could then be gathered into yearly volumes with predictable, structured regularity. But if this makes the later eighteenth century the “age of the annual,” it was also the age of the centurial, and the historical moment when the interplay between the annual and the centurial assumed an enhanced importance. “The use of centuries as time designations,” as Lynn Hunt notes, “only became common in the seventeenth century, at least in English and French” (119), and this manner of comprehending time assumed increased explanatory power in the eighteenth century.
When, for example, in The Wealth of Nations book two, Adam Smith confronted the regular appearance of jeremiads predicting British decline, he insisted on the need to identify quantifiable economic criteria through which decline might be measured (national production in his case), but he also emphasized the need to calibrate one’s temporal perspective away from the annual and immediate and upwards to the unit of the century. Smith explains this point by looking at the many disasters and set-backs of post-Restoration Britain, events that, in his reading, have been counteracted by what he describes as “gradal” progress that is “not only not sensible” but that also sometimes produces the suspicion of decay. Calibrating one’s perspective for the longer term of the century, Smith insists, allows one to “form a right judgment” (365).
Playfair was a keen and avid reader of Smith, and he edited the controversial eleventh edition of The Wealth of Nations, the first critical edition of the work in which he repeatedly took issue with many of Smith’s claims.[14] Playfair’s work develops Smith’s insistence on the move from the smaller scale to the larger scale, from the annual to the centurial; his charts not only enable their users to link the particular data of a year to a pattern spread across a century but also they assume in their very form and scale that all annual data must be subsumed into the larger pattern of the century. Time, which many in the later eighteenth century felt to be accelerating, could be made to yield to measured regularity. In these ways, then, Playfair’s graphic charts and his method of lineal arithmetic would seem to crystallize his moment. Nonetheless, despite Playfair’s repeated publication of his charts and graphs in edition after edition of the Commercial and Political Atlas and other publications like the Statistical Breviary and his reuse of certain graphics in the Inquiry, one remarkable feature of Playfair’s ingenuity was its failure to catch on.[15]
But if, as this entry has suggested, Playfair’s techniques for the visualization of economic and financial process over time were of their moment, why did they languish for so long before being taken up by others? Scholars often note that Playfair’s personality and moral shortcomings made his work unpalatable to his intended audience of MPs and financial men.[16] In addition, since Playfair did not include in his publications the raw data tables on which his graphics were based, it would have been difficult to evaluate the accuracy of his charts—indeed, recent work has insisted on considerable discrepancy between Playfair’s curves and his raw data.[17] These are explanations particular to Playfair. Another account focuses on the history of statistics and suggests that the graphic method became more important as political arithmetic and data collection merged with the theory of probabilities and as statistics grew more and more into a scientific discipline.[18]
We might also think here about the relationship between Cartesian geometry and Playfair’s graphics. Descartes’ introduction of the coordinate system in 1637 is clearly a fundamental precondition for Playfair’s work. But, with a small number of exceptions, Cartesian geometry was used for the formal representation of abstract mathematical functions, and graphs came to be considered applicable only where formal geometry was applicable. Playfair’s graphs, in contrast, are based not on abstract mathematics but on the compilation of unique, particular, and non-repeatable data. They also require only minimal geometry. It is therefore possible, as Albert Biderman insists, that formal mathematical geometry served as a “downright obstacle” to graphic statistics (11).
There was, furthermore, a deeply ingrained prejudice against images or charts amongst English scientific and economic thinkers. While we may take for granted the value of graphs for conveying information and analysis, this was not always the case; such illustrations were seen by most in the eighteenth and early nineteenth centuries as works of imagination, not science, and consequently as lacking intellectual seriousness. John Bender and Michael Marrinan suggest that there are fundamentally epistemological reasons for this and note, “Lockeans distrusted graphs along with language as conventional constructs of limited descriptive power. Graphs plotted by instruments did not escape the hermeneutics of deception” (55). They continue to observe the contrast between this empiricist mistrust of graphs and a less suspicious continental tradition following Leibniz and Johann Heinrich Lambert that “viewed graphs as the potential basis for a universal language of description” (55)—the very sort of terms that, as we have seen, Playfair uses to recommend his results to “a native of another country” in his 1801 preface to the Atlas (v).
But there is, finally, an additional explanation for the failure of Playfair’s graphs to take hold in England, namely that they required a fundamentally different understanding of date and event from that current in the later eighteenth and early nineteenth centuries. As discussed in the opening of this entry, a traditional understanding of an historical event like the French Revolution or the English Civil War typically seeks to investigate and order all of its contributing motivations and causes into a unique narrative and discursive account. Playfair’s graphs, in contrast, focus not on a singular and unique event but on comparable and recurring events in time. A statistical chart like those pioneered by Playfair requires not just the abundant data collection that marked the eighteenth century but also an understanding of the interplay between date and event such that its episodes (the trade balance between France and England, say) can be repeated and broken down into equal units (years) across the horizontal time-axis and also that the quantity (pounds sterling) measured across time on the vertical axis can be homogenous enough to sustain comparison. It requires that dates be considered as data. An “event,” such renderings imply, is less a complex, overdetermined series of discernible and interlinked causes and intentions but rather a comparable and recurring series of similar occurrences in time by which episodes that seem to lack significance in and of themselves attain meaning when aggregated. In other words, Playfair’s charts are similar to the narrative and discursive model of history in that they also might be understood to construct the events they present as significant. Such constructions, however, occur not through narrative but rather through the graphic representation of data, which is understood to reveal unseen patterns in the collection and connection of an otherwise isolated set of facts. As Harro Maas and Mary S. Morgan note, “Playfair’s lineal arithmetic of graphs scaled economic life in monetary terms and in time units” and thus revealed a new kind of event: “the movement of a homogenous entity, money, through time” (106, 105). For the explanatory powers of such a chart to take hold requires an expansion in the understanding of history and event, not only one attuned to the widespread discursive understanding of history associated with events like the French Revolution in the example above, but also one that could understand, say, the trade balance of England and France as a potentially significant event (or series of events) with its own explanatory power.
HOW TO CITE THIS BRANCH ENTRY (MLA format)
published October 2012
Sachs, Jonathan. “1786/1801: William Playfair, Statistical Graphics, and the Meaning of an Event.” BRANCH: Britain, Representation and Nineteenth-Century History. Ed. Dino Franco Felluga. Extension of Romanticism and Victorianism on the Net. Web. [Here, add your last date of access to BRANCH].
WORKS CITED
Bender, John and Michael Marrinan. The Culture of Diagram. Stanford UP, 2010. Print.
Biderman, Albert. “The Playfair Enigma: The Development of the Schematic Representation of Statistics.” Information Design Journal 6: 3-25. Print.
De Bruyn, Frans. “From Georgic Poetry to Statistics and Graphs: Eighteenth-Century Representations and the ‘State’ of British Society.” The Yale Journal of Criticism 17.1 (2004): 107-39. Print.
Dunyach, Jean-François. “Les Réseaux Excentrique: Vies et Parcours de William Playfair (1759-1823).” Cultural Transfers: France and Britain in the Long Eighteenth Century. Studies on Voltaire and the Eighteenth Century 4. Eds. Ann Thomson, Simon Burrows, and Edmond Dziembowski. Oxford: Oxford UP, 2010. 115-127. Print.
Funkhauser, H. Gray. “Historical Development of the Graphical Representation of Statistical Data.” Osiris 3 (1937): 269-404. Print.
Goodison, Nicholas. “Lunar Society Correspondence.” May 1993. The Industrial Revolution: A Documentary History. Ed. Jennifer Tann. Adam Matthew Publications. Adam Matthew Digital Ltd., 2012. Web. 22 Sept. 2012.
Grafton, Anthony and Daniel Rosenberg. Cartographies of Time: A History of the Timeline. Princeton: Princeton Architectural Press, 2010. Print.
Grossman, Henryk. “W. Playfair, the Earliest Theorist of Capitalist Development.” The Economic History Review. 18 (1948): 65-83. Print.
Hunt, Lynn. Measuring Time, Making History. Budapest: Central European UP, 2008. Print.
Koselleck, Reinhart. Futures Past: On the Semantics of Historical Time. Trans. Keith Tribe. Cambridge: MIT Press, 1985. Print.
Maas, Harro and Mary S. Morgan. “Timing History: The Introduction of Graphical Analysis in 19th-Century British Economics.” Revue d’Histoire des Sciences Humaines 7 (2002): 97-127. Print.
Playfair, William. The Commercial and Political Atlas. London, 1786. Print.
Playfair, William. The Commercial and Political Atlas. 3rd ed. London, 1801. Print.
Playfair, William. Inquiry into the Permanent Causes of the Decline and Fall of Powerful and Wealthy Nations. London, 1805. Print.
Playfair, William. The Statistical Breviary. London, 1801. Print.
Priestley, Joseph. Chart of Biography. London, 1765. Print.
Priestley, Joseph. A New Chart of History. London, 1769. Print.
Rees-Mogg, William, ed. Adam Smith: An Inquiry into the Nature and Causes of the Wealth of Nations: Edited by William Playfair. London: Pickering and Chatto, 1995. Print.
Rosenberg, Daniel. “Joseph Priestley and the Graphic Invention of Modern Time.” Studies in Eighteenth-Century Culture 36 (2007): 55-103. Print.
Royston, Erica. “Studies in the History of Probability and Statistics: III. A Note on the History of the Graphical Presentation of Data.” Biometrika, 43 (1956), 241-247. Print.
Smith, Adam. An Inquiry into the Nature and Causes of the Wealth of Nations. Ed. Edwin Cannan. Chicago: U of Chicago P, 1976. Print.
Smith, Adam. Lectures on Jurisprudence. Indianapolis: The Liberty Fund, 1982. Print.
Spence, Ian and Howard Wainer. “William Playfair: A Daring Worthless Fellow.” Chance 10.1 (1997): 31-35. Print.
Spence, Ian and Howard Wainer, “Introduction.” The Commercial and Political Atlas and Statistical Breviary. Eds. Spence and Wainer. Cambridge: Cambridge UP, 2005. Print.
Spence, Ian. “Playfair, William (1759–1823).” Oxford Dictionary of National Biography. Oxford UP, 2004. Web. 3 May 2011.
—. “William Playfair and the Psychology of Graphs.” Proceedings of the American Statistical Association, Section on Statistical Graphics. Alexandria: American Statistical Association, 2006. 2426-2436. Print.
Stigler, Stephen M. Statistics on the Table: The History of Statistical Concepts and Methods. Cambridge: Harvard UP, 1999. Print.
Tucker, Herbert F. “On Event.” BRANCH: Britain, Representation and Nineteenth-Century History. Ed. Dino Franco Felluga. Extension of Romanticism and Victorianism on the Net. Web. Accessed 11 June 2012.
Tufte, Edward R. The Visual Display of Quantitative Information. Cheshire: Graphics Press, 1983. Print.
Uglow, Jenny. The Lunar Men: Five Friends Whose Curiosity Changed the World. New York: Farar, Strauss and Giroux, 2002. Print.
ENDNOTES
[1] In addition to Tucker, for a particularly lucid and thoughtful reflection on narrative ordering and the relativity of historical eventfulness, see Hunt 26-29.
[2] Playfair’s Commercial and Political Atlas (1786, with new editions in 1787 and 1801) consists mostly of time-series line graphs with one bar chart, while the circle chart and the pie chart debut in his Statistical Breviary (1801). There is a fair amount of secondary literature on Playfair, most of which is rooted in the history of statistics, and most of which accords him considerable influence and primacy in the history of statistical graphics. For my account of Playfair’s work, the following have been the most useful: Tufte, Biderman, Maas and Morgan.
[3] For a discussion of Jevons as a statistician, and his development of statistical graphics, see Stigler 66-79.
[4] The Dutchman Christiaan Huygens used John Graunt’s data on English mortality rates to construct a rudimentary time-series graph of the data in a letter to his brother in 1669. See Biderman for the claim that “neither the Cartesian system, nor any geometry that did not exist before Euclid was at all needed for any of Playfair’s forms” (11). This is part of Biderman’s larger argument that formal mathematical geometry was likely an impediment to the development of statistical graphing, which relied on raw as opposed to abstract data.
[5] This account of Playfair’s life and work is based on the entry by Ian Spence in the online-version of the Oxford Dictionary of National Biography. See also Dunyach. On Playfair’s early influences, see Spence, 2006, 2427-29.
[6] For a comprehensive account of the differences between the three editions of the Atlas, see Spence and Wainer, 2005, 16-23.
[7] For a provocative reading of the links between cartography, the prospect view, Playfair’s graphs, and the georgic genre, see de Bruyn.
[8] On Priestley and the timeline, see Rosenberg.
[9] Boulton, Watt, and Priestley were all members of the Lunar Society in Birmingham. As an apprentice draughtsman, Playfair was not a member, though he worked closely enough with Watt to merit a mention in at least two letters, one from Watt to Boulton in 1778 (Spence and Wainer, 2005, 5) and another from the chemist James Keir to Boulton in 1777 (qtd. in Goodison). On late eighteenth-century intellectual life in the British Midlands and the Lunar Society of Birmingham, see Uglow.
[10] For more on Playfair and the psychology of graphs, see Spence, 2006.
[11] This was one of Playfair’s most significant differences from Adam Smith, who did not consider balance of trade to be a significant economic indicator. See Smith Wealth of Nations book IV, especially chapter 3, 496-524 and Smith Lectures on Jurisprudence 388-394, 511-19.
[12] The German A. F. W. Crome preceded Playfair in translating geographic areas into proportioned geometric shapes, in his case squares. On the relationship between Playfair and Crome, see Royston.
[13] Playfair also drew a sloped line between population and revenue meant to indicate the approximate rate of tax, but this would, of course, be inaccurate since the slope of the line would depend on the relative diameters of the circles and the height difference in the ordinates. On this point, see Funkhauser 285. Also, see Spence and Wainer, 2005, 28 and Royston 245.
[14] For a recent publication of this 1805 edition, see Adam Smith: An Inquiry into the Nature and Causes of the Wealth of Nations: Edited by William Playfair, ed. William Rees-Mogg.
[15] In later editions, Playfair—who, as the brief sketch of his life above suggests, was in a number of his ventures something of a con man, or, in the words of one solicitor, “a daring worthless fellow” (qtd. by Spence and Wainer, 1997, 34—insisted that his work was widely recognized and cited Dr Gilbert Stuart from The Political Herald to the effect that “The new method in which accounts are stated in this work has attracted very general notice” (Atlas, 1801, vii-viii). But as late as 1937, a history of graphic representation noted the “common opinion shared by layman and statistician alike, that the graphic method in statistics is of recent origin” (Funkhouser 270). The author explains that, despite Playfair’s attempt to articulate the value of his charts and to popularize their use, through the first half of the nineteenth century, English statistical publications ignored charts in favor of tables of figures: “The Journal of the London Statistical Society was established in 1837. Graphs began to appear in it in 1841. In the first fifty volumes graphic representations occur fourteen times. Nine of these deal with vital statistics. The first graphs of economic data in this journal appeared in 1847 and are crudely drawn” (294). Not surprisingly, Playfair remained uncited by an English statistician or economist until William Jevons insisted to the ![]() London Statistical Society in 1879 that “Englishmen have lost sight of the fact that William Playfair who has never been heard of in this generation produced statistical atlases and statistical curves that ought to be treated by some writer in the same way that Dr Guy has treated the method of Dr Todd” (qtd. in Funkhouser, 293).
London Statistical Society in 1879 that “Englishmen have lost sight of the fact that William Playfair who has never been heard of in this generation produced statistical atlases and statistical curves that ought to be treated by some writer in the same way that Dr Guy has treated the method of Dr Todd” (qtd. in Funkhouser, 293).
[16] This is a point made by Spence and Wainer, 1997, 31 and Funkhouser 292.
[17] See, for example, Spence and Wainer, 2005, 18.
[18] See Funkhouser 291-92.